Heaps are a specialized tree-based data structure primarily implemented in priority queues and efficient sorting algorithms. They are binary trees that maintain a specific order between parent and child nodes, which makes them ideal for certain types of data access operations, such as quickly finding the minimum or maximum element.
Table of Contents
What is Heap Data Structure?
A heap is a binary tree-based data structure that follows the heap property. In a heap, the value of each node is compared to the values of its children in a specific way
Heap property
- Min Heap: The value of each node is less than or equal to its children’s values. The smallest value is found at the root of the tree.
- Max Heap: The value of each node is greater than or equal to its children’s values. The largest value is at the root.
This property guarantees that the largest (in a max-heap) or smallest (in a min-heap) value is always at the root, and the tree maintains a specific order based on the heap type.
Types of Heaps
There are two main types of heaps:
- Max Heap: The root node contains the maximum value, and the values decrease as you move down the tree.
- Min Heap: The root node contains the minimum value, and the values increase as you move down the tree.
Power of heap
| Data Struture/Operation | Insert | Search | Find min/max | Delete min/max |
| Unsorted Array | O(1) | O(N) | O(N) | O(N) |
| Sorted Array | O(N) | O(logN) | O(1) | O(N) |
| Linked list | O(1) | O(N) | O(N) | O(N) |
| Heap | O(logN) | O(N) | O(1) | O(logN) |
- A sorted array and a heap can find the maximum or minimum element in O(1) time among the data structures listed. However, a heap has an O(log N) time complexity for both insertion and deletion, whereas a sorted array has an O(N) time complexity for these operations
Also, read about time complexity
Representation of Heap
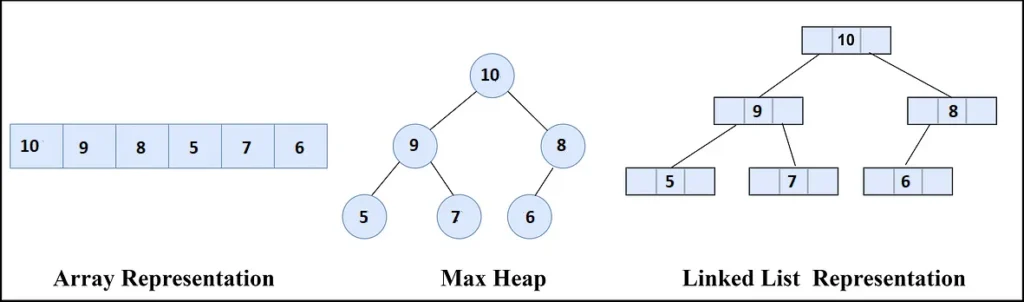
Heaps are typically represented in a few different ways, depending on the context and use case. Here are the most common methods:
Array Representation
Arrays are the most commonly used representation for heaps. They are both space-efficient and simple to implement.
Array Representation Rules:
For a node at index i:
- The left child is at index 2i + 1
- The right child is at index 2i + 2
For a child at index i:
- The parent is at index (i-1) // 2
- // To take whole number only
Linked List Representation
Each node in the heap is represented using a class with a value and references to its left and right child nodes. It offers flexibility for dynamic resizing but may require more memory due to node references.
List of Lists
In some contexts, heaps are represented using a list of lists, where each sublist contains the children of the node:
[
[10], # Root node
[9, 8], # Level 1
[5,7,6] # Level 2
]
Array is the most commonly used representation.
Heap Operations
Common heap operations are:
- Insert: Adds a new element to the heap while maintaining the heap property. Read
- Extract(deletion) Max/Min: Removes the maximum or minimum element from the heap and returns it. Read
- Heapify: Converts an arbitrary binary tree into a heap.
# Max-Heap data structure in Python
def heapify(arr, n, i):
largest = i
l = 2 * i + 1
r = 2 * i + 2
if l < n and arr[l] > arr[largest]:
largest = l
if r < n and arr[r] > arr[largest]:
largest = r
if largest != i:
arr[i], arr[largest] = arr[largest], arr[i]
heapify(arr, n, largest)
def deleteNode(array, num):
size = len(array)
i = 0
for i in range(size):
if array[i] == num:
break
# Swap with the last element
array[i], array[-1] = array[-1], array[i]
array.pop() # Remove the last element which is now the number to be deleted
# Only run heapify if the deleted node was not the last node
if i < len(array):
heapify(array, len(array), i)
def insert(array,newNum):
array.append(newNum)
current = len(array)-1
while current > 0:
parent = (current-1) // 2
if array[current]>array[parent]:
array[current],array[parent] = array[parent],array[current]
current = parent
else:
break
arr = []
insert(arr,3)
print("Inserting element:",arr)
insert(arr,2)
print("Inserting element:",arr)
insert(arr,5)
print("Inserting element:",arr)
insert(arr,6)
print("Inserting element:",arr)
insert(arr,7)
print("Inserting element:",arr)
insert(arr,15)
print("Inserting element:",arr)
insert(arr,9)
print("Inserting element:",arr)
insert(arr,1)
print("Inserting element:",arr)
insert(arr,8)
print("Inserting element:",arr)
deleteNode(arr, 6)
print("After deleting an element:", arr)
deleteNode(arr, 9)
print("After deleting an element:", arr)
deleteNode(arr, 8)
print("After deleting an element:", arr)
deleteNode(arr, 15)
print("After deleting an element:", arr)
deleteNode(arr, 2)
print("After deleting an element:", arr)
deleteNode(arr, 7)
print("After deleting an element:", arr)
deleteNode(arr, 1)
print("After deleting an element:", arr)
#Output
Inserting element: [3]
Inserting element: [3, 2]
Inserting element: [5, 2, 3]
Inserting element: [6, 5, 3, 2]
Inserting element: [7, 6, 3, 2, 5]
Inserting element: [15, 6, 7, 2, 5, 3]
Inserting element: [15, 6, 9, 2, 5, 3, 7]
Inserting element: [15, 6, 9, 2, 5, 3, 7, 1]
Inserting element: [15, 8, 9, 6, 5, 3, 7, 1, 2]
After deleting an element: [15, 8, 9, 2, 5, 3, 7, 1]
After deleting an element: [15, 8, 7, 2, 5, 3, 1]
After deleting an element: [15, 5, 7, 2, 1, 3]
After deleting an element: [7, 5, 3, 2, 1]
After deleting an element: [7, 5, 3, 1]
After deleting an element: [5, 1, 3]
After deleting an element: [5, 3]Heap Data Structure Applications
Heaps have various applications, like:
- Heaps are commonly used to implement priority queues, where elements are retrieved based on their priority (maximum or minimum value).
- Heapsort is a sorting algorithm that uses a heap to sort an array in ascending or descending order.
- Heaps are used in graph algorithms, such as Dijkstra’s and Prim’s, to find the shortest paths and minimum spanning trees.
- Median Finding: A min heap can be used to efficiently find the median of a stream of numbers. We can use one min heap to store the larger half of the numbers and one max heap to store the smaller half. The median will be the root of the min heap. Also, see